TESORAX

Instagram Linkedin

MENU

en_GB
en_GB fr_FR

LITZ WIRES

Home
LITZ WIRES

THE FUTURE OF HIGH FREQUENCY EQUIPMENTS CONNECTION

DESCRIPTION OF LITZ WIRES

Used in high frequency current carrying applications, Litz wires are constructed with small diameter (0.04mm to 5mm) enameled copper wires, electrically insulated and braided from each other to reduce losses called "skin effect*", generated by opposing electromagnetic currents (Eddie currents). At low frequencies, this phenomenon is considered negligible, although some energy conversion specialists believe that losses are evident from low frequencies.

WHY ENAMELLED COPPER WIRES?

With simple copper wires, which have low resistance, electric current will tend to flow around the periphery of the conductor. The impedance will then increase, and the percentage loss will increase as the impedance increases, finding that the increase in resistance will grow much faster than the increase in section. The use of multi-stranded wires makes it possible to reduce losses thanks to the reduction of the HF resistance, by skin effect and eddy current. It is thus understood that the use of simple copper wires in modern equipment such as transformers, electromagnets or alternators can lead to catastrophes. The cables are constructed so that "proximity effect" losses are also reduced. We will also choose the type of varnish according to the temperature class (from 150 to 240°C).

Note that the diameter of the unitary wire will be chosen according to the frequency at which it is desired to work, so that their diameter is smaller than the thickness of the skin. See table below.

APPLICATIONS

Mainly used for power conversion, high frequency transmission and reception, power electronics, inductive proximity switches, electronic tags, multiple telephone transmission equipment, coil windings, flexible connections for relays, coils, transformers, motors, etc.

Our manufacturing site based in Spain enables international delivery of our solutions. We also offer unitary enamelled copper wires.

Why use Litz Wires?

Technical specifications

Litz cables can be manufactured in different ways according to the recommendations of the Design Office. TESORAX manufactures them with the wires assembled in the same direction and with a strand pitch less than 60mm. On request, and to meet the needs of our customers, we can form them in rectangular or square section in order to reduce the winding volume. Our Litz cables are manufactured using materials that allow direct welding without the need for a mechanical procedure. Before soldering, the Litz cable must be immersed in a pickling agent and then in a bath of tin (60%) and lead (40%) at a temperature of 375°C to 400°C. The immersion time depends on the number of wires and the diameter of the cable.

Winding losses

The losses produced in the coils are due to the factors:

  • Losses in the conductor:

    • Joule effect

    • Eddy currents

  • Capacity losses

  • Losses due to the hysteresis effect of the core

The first two factors appear in the coils and the third in those having a ferromagnetic core. We will analyze the first two factors in order to justify the use of the Litz cable.

Losses in the conductor

The Joule effect is known that electrical conductors heat up by the passage of current, which has the effect of increasing the ohmic resistance of the conductor and therefore reducing the possible current in the same section. Apparently, it is possible to increase the section in order to decrease the Joule effect, but this would lead to an increase in losses due to eddy currents. Changing the section is therefore not a solution, once it has been defined. We can do as follows: once the section of the conductor has been determined, in order to eliminate the film effect, we can join together, at the calculated section, enamelled cables; in this way we obtain a section which will be maintained during the whole working cycle of the coil. The thinner the threads, the better the result, due to the dandruff effect. However, this solution is expensive. We recommend the ideal calculation of the cross-section which can be studied on a case-by-case basis by a technician. To calculate the skin current, use the following formula which gives us the current level (depth):
Pour calculer le courant pelliculaire, utiliser la formule suivante qui nous donne le niveau (profondeur) de courant:

F1_edited.png

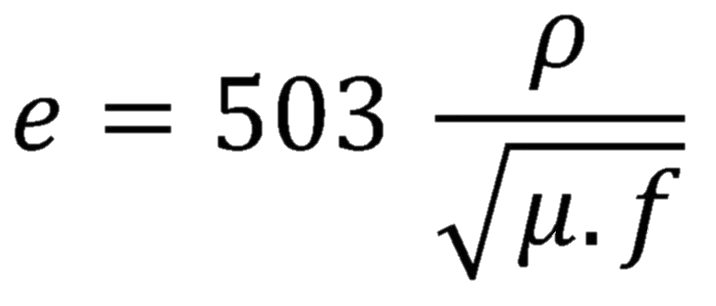
e = Thickness to be calculated // p = Resistivity of the conductor
u = Permeability of the conductive material // f = Current frequency

For a copper conductor, the formula takes the following form:

F2_edited.png
The value is given in millimeters.

The resistance of an alternating current conductor is given by:

F3_edited_edited.png

 I = Perimeter in mm of the conductor section.
For copper, the formula becomes:

F4_edited_edited.png

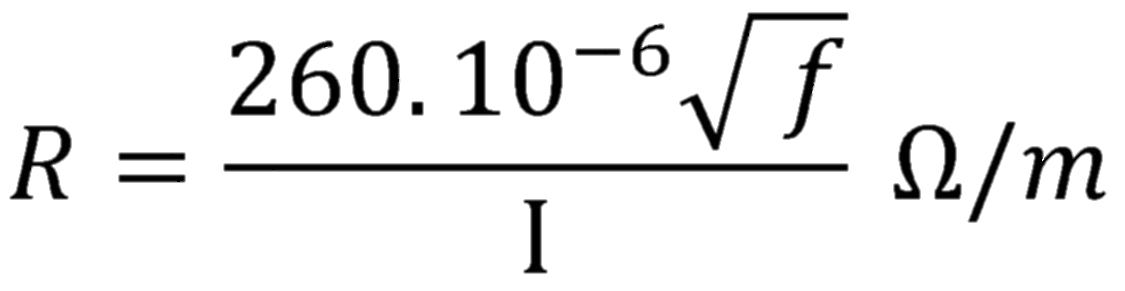
Eddy currents

When a ferromagnetic material is introduced into an alternating magnetic field, in addition to magnetization, an induced voltage is created; this produces an induced current which depends on the resistivity of the material. The current induced in the material is consumed in the form of heat (Joule effect) which is given by the formula:
 

F5_edited_edited.png

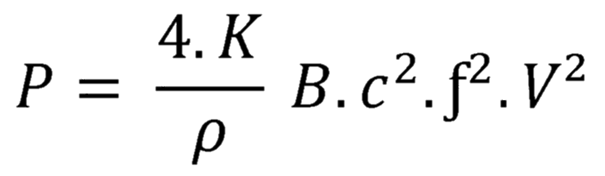
  P = Power dissipated by eddy currents // K = Constant p = Resistivity of copper // B = Maximum induction passing through the material c = Thickness of the ferromagnetic material // f = Frequency // V = Volume of the ferromagnetic material  

Capacity losses

Two conductors with different potentials accumulate electrical energy at the same time. The wires used in the manufacture of coils have this particularity, which allows us to speak of a sum of capacities distributed between the various turns of this one. The coils studied are subjected to an alternating voltage of high frequency, close to the resonant frequency which gives us a very high impedance as if they were in parallel with the ohmic resistance and the self-inductive coefficient of the coil. These concepts give us the conclusion that the capacity of the coil alone is equal to 0.55 times its diameter in cm. We can change the capacity of the coil by:
  • Studying its dimensions
  • Chercher le meilleur enroulement
  • Distributing the currents in the coil and Insulating the conductors
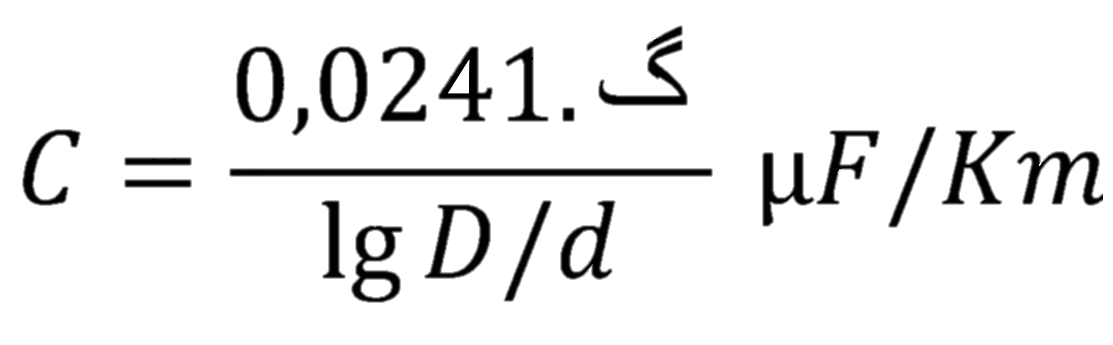
The capacitance between two conducting wires is: F6_edited_edited.png گ = Dielectric constant of the insulation // D = Diameter of the wire with the insulation // d = Diameter of the bare wire Une fois l’isolant choisi – qui doit avoir une constante diélectrique très faible et doit répondre à nos objectifs – nous devons analyser la relation D/d. Plus elle est faible, meilleure sera la capacité. L’ingénieur doit décider de la meilleure solution en tenant compte du courant maximum devant passer au travers chaque fil et de la tension supportée par les fils. Un toronnage adéquat des fils formant le câble de Litz donnera l’uniformité nécessaire à la distribution capacitive à travers ce câble, de telle manière à augmenter le facteur de qualité de la bobine. En plaçant une spirale de soie naturelle, polyester ou toute autre fibre qui répond à nos spécifications, comme support au toronnage de fils émaillés, nous n’augmentons pas le facteur D. De plus le pas de spire de la fibre doit être parfait dimensionné pour que les câbles de Litz ne soient pas trop rigides, afin de permettre un bon bobinage sans augmenter l’inductance apparente créée entre les spirales. La relation IgD/d est un facteur multipliant pour l’inductance et doit être le plus petit possible, et est un facteur divisant pour la capacité pour lequel il doit être le plus grand possible. It is up to the engineer who calculates the coil to determine the parameters to be considered in the study of the circuit:
  • Ohmic resistance
  • Total induction
  • Total capacity
 

The end result should be a coil ready for use in the circuit, with the best performance, lowest volume, and best quality while having the lowest resistance loss.

Litz cables are used to:
  • Reduce losses by Joule effect
  • Reduce losses due to eddy currents
  • Use smaller magnetic cores
  • Obtain capacity in small coils
  • Get better quality
  • Easy handling of cables for winding, due to wires fixed together
  • Extra-flexible cables allowing core winding with a very small bend radius

Manufacturing standards

TESORAX ensures the manufacture according to the DIN 46.447 standard, and studies the cables according to the criteria:

  • Number of wires depending on the cable diameter
  • The type of insulation
  • The support system
  • Enamelled copper must be tinned. The outside diameter and other properties of the enamelled copper wire are selected by the manufacturer if the customer does not formally specify them. The outside diameter without insulation is the basis for calculating the outside diameter of the insulated cable: this is not used during reception checks.
High frequency cables (Litz cables) are defined by:
  • Thickness of each elementary wire
  • Total number of wires and bundling
  • No stranding
  • Insulating

The DIN 46.447 standard defines the types of cables according to each of these 4 criteria. Any question about the effective cross section of the conductor is defined as follows:

  • Preset effective section: 0.70mm²
  • Individual wire diameter: 0.10mm, i.e. a section of 0.007854 mm²
  • Corresponding number of threads: 0.70 / 0.007854 = 89.13 theoretical threads. 90 threads will be used. The studied cable will have the following composition: 90x 0.10mm
 

Do not hesitate to contact us for any information: Our design office will be able to guide you in the cable solution that suits you best.